El álgebra elemental es una fundamental y relativamente básica forma de álgebra enseñada a los estudiantes que se presumen tienen poco o nada de conocimiento formal de las matemáticas más allá de la aritmética. Mientras que en aritmética solo ocurren los números y sus operaciones aritméticas elementales (como +, -, ×, ÷), en álgebra también se utilizan símbolos para denotar números (como x, y, a y b). Éstos son llamados variables. Esto es útil porque:
- Permite la generalización de ecuaciones aritméticas (y de inecuaciones) para ser indicadas como leyes (por ejemplo
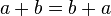 para toda
para toda  y
y  ), y es así el primer paso al estudio sistemático de las propiedades del sistema de los números reales.
), y es así el primer paso al estudio sistemático de las propiedades del sistema de los números reales. - Permite la referencia a números que no se conocen. En el contexto de un problema, una variable puede representar cierto valor que todavía no se conoce, pero que puede ser encontrado con la formulación y la manipulación de las ecuaciones.
- Permite la exploración de relaciones matemáticas entre las cantidades (por ejemplo, “si usted vende x boletos, entonces, su beneficio será 3x - 10 dólares”).
Estas tres son los hilos principales del álgebra elemental, que deben ser distinguidos del álgebra abstracta, un tema más avanzado enseñado generalmente a los estudiantes universitarios.
En álgebra elemental, una expresión puede contener números, variables y operaciones aritméticas. Por convención, éstos generalmente se escriben con los términos con exponente más altos a la izquierda (ver polinomio); algunos ejemplos son:
Una ecuación es la aseveración de que dos expresiones son iguales. Algunas ecuaciones son verdades para todos los valores de las variables implicadas (por ejemplo 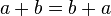 ); tales ecuaciones son llamadas identidades. Las ecuaciones condicionales son verdades para solamente algunos valores de las variables implicadas:
); tales ecuaciones son llamadas identidades. Las ecuaciones condicionales son verdades para solamente algunos valores de las variables implicadas:  . Los valores de las variables que hacen la ecuación verdadera se llaman las soluciones de la ecuación.
. Los valores de las variables que hacen la ecuación verdadera se llaman las soluciones de la ecuación.
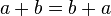 ); tales ecuaciones son llamadas identidades. Las ecuaciones condicionales son verdades para solamente algunos valores de las variables implicadas:
); tales ecuaciones son llamadas identidades. Las ecuaciones condicionales son verdades para solamente algunos valores de las variables implicadas:  . Los valores de las variables que hacen la ecuación verdadera se llaman las soluciones de la ecuación.
. Los valores de las variables que hacen la ecuación verdadera se llaman las soluciones de la ecuación.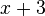


No hay comentarios:
Publicar un comentario