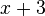LAS TIC
martes, 5 de octubre de 2010
Para otros usos de este término, véase Ángulo (desambiguación).
Los ángulos son la parte del plano comprendida entre dos semirrectas que tienen el mismo origen.[1] Suelen medirse en unidades tales como el radián, el grado sexagesimal o el grado centesimal.Pueden estar definidos sobre superficies planas (trigonometría plana) o curvas (trigonometría esférica). Se denomina ángulo diedro al espacio comprendido entre dos semiplanos cuyo origen común es una recta. Un ángulo sólido es el que abarca un objeto visto desde un punto dado, midiendo su tamaño aparente.
[editar] Definiciones
Existen básicamente dos formas de definir un ángulo en el plano- Forma geométrica: Se denomina ángulo a la amplitud entre dos líneas de cualquier tipo que concurren en un punto común llamado vértice. Coloquialmente, ángulo es la figura formada por dos líneas con origen común. El ángulo entre dos curvas es el ángulo que forman sus rectas tangentes en el punto de intersección.
- Forma trigonométrica: Es la amplitud de rotación o giro que describe un segmento rectilíneo en torno de uno de sus extremos tomado como vértice desde una posición inicial hasta una posición final. Si la rotación es en sentido levógiro (contrario a las manecillas del reloj), el ángulo se considera positivo. Si la rotación es en sentido dextrógiro (conforme a las manecillas del reloj), el ángulo se considera negativo.
[editar] Definiciones clásicas
Euclides define un ángulo como la inclinación mutua de dos líneas que se encuentran una a otra en un plano y no están en línea recta. Según Proclus un ángulo debe ser una calidad o una cantidad, o una relación. El primer concepto fue utilizado por Eudemus, que describió un ángulo como desviación de una línea recta; el segundo por Carpus de Antioch, que lo vio como el intervalo o el espacio entre las líneas que se intersectaban; Euclides adoptó un tercer concepto, aunque sus definiciones de ángulos rectos, agudos, y obtusos son cuantitativas.[editar] Las unidades de medida de ángulos
Las unidades utilizadas para la medida de los ángulos del plano son:- Radián (usado oficialmente en el sistema internacional de unidades)
- Grado centesimal
- Grado sexagesimal
[editar] Clasificación de ángulos
Los ángulos, de acuerdo con su amplitud, reciben estas denominaciones:
Las manijas de un reloj conforman distintos tipos de ángulos. En este caso, un ángulo agudo.
| Tipo | Descripción |
|---|---|
| Ángulo nulo | Es el ángulo formado por dos semirrectas coincidentes, por lo tanto su abertura es nula, o sea de 0°. |
Ángulo agudo  | Es el ángulo formado por dos semirrectas con amplitud mayor de 0 rad y menor de  rad. Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o menor de 100g (grados centesimales). rad. Es decir, mayor de 0° y menor de 90° (grados sexagesimales), o menor de 100g (grados centesimales). |
Ángulo recto 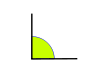 | Un ángulo recto es de amplitud igual a  rad Es equivalente a 90° sexagesimales (o 100g centesimales). rad Es equivalente a 90° sexagesimales (o 100g centesimales).Los dos lados de un ángulo recto son perpendiculares entre sí. La proyección ortogonal de uno sobre otro es un punto, que coincide con el vértice. |
Ángulo obtuso  | Un ángulo obtuso es aquel cuya amplitud es mayor a  rad y menor a rad y menor a  rad Mayor a 90° y menor a 180° sexagesimales (o más de 100g y menos de 200g centesimales). rad Mayor a 90° y menor a 180° sexagesimales (o más de 100g y menos de 200g centesimales). |
| Ángulo llano o colineal  | El ángulo llano tiene una amplitud de  rad Equivalente a 180° sexagesimales (o 200g centesimales). rad Equivalente a 180° sexagesimales (o 200g centesimales).También es conocido como ángulo extendido. |
| Ángulo completo o perigonal  | Un ángulo completo o perigonal, tiene una amplitud de  rad Equivalente a 360° sexagesimales (o 400g centesimales). rad Equivalente a 360° sexagesimales (o 400g centesimales). |
la algebra elemental
El álgebra elemental es una fundamental y relativamente básica forma de álgebra enseñada a los estudiantes que se presumen tienen poco o nada de conocimiento formal de las matemáticas más allá de la aritmética. Mientras que en aritmética solo ocurren los números y sus operaciones aritméticas elementales (como +, -, ×, ÷), en álgebra también se utilizan símbolos para denotar números (como x, y, a y b). Éstos son llamados variables. Esto es útil porque:
- Permite la generalización de ecuaciones aritméticas (y de inecuaciones) para ser indicadas como leyes (por ejemplo
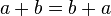 para toda
para toda  y
y  ), y es así el primer paso al estudio sistemático de las propiedades del sistema de los números reales.
), y es así el primer paso al estudio sistemático de las propiedades del sistema de los números reales. - Permite la referencia a números que no se conocen. En el contexto de un problema, una variable puede representar cierto valor que todavía no se conoce, pero que puede ser encontrado con la formulación y la manipulación de las ecuaciones.
- Permite la exploración de relaciones matemáticas entre las cantidades (por ejemplo, “si usted vende x boletos, entonces, su beneficio será 3x - 10 dólares”).
Estas tres son los hilos principales del álgebra elemental, que deben ser distinguidos del álgebra abstracta, un tema más avanzado enseñado generalmente a los estudiantes universitarios.
En álgebra elemental, una expresión puede contener números, variables y operaciones aritméticas. Por convención, éstos generalmente se escriben con los términos con exponente más altos a la izquierda (ver polinomio); algunos ejemplos son:
Una ecuación es la aseveración de que dos expresiones son iguales. Algunas ecuaciones son verdades para todos los valores de las variables implicadas (por ejemplo 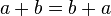 ); tales ecuaciones son llamadas identidades. Las ecuaciones condicionales son verdades para solamente algunos valores de las variables implicadas:
); tales ecuaciones son llamadas identidades. Las ecuaciones condicionales son verdades para solamente algunos valores de las variables implicadas:  . Los valores de las variables que hacen la ecuación verdadera se llaman las soluciones de la ecuación.
. Los valores de las variables que hacen la ecuación verdadera se llaman las soluciones de la ecuación.
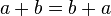 ); tales ecuaciones son llamadas identidades. Las ecuaciones condicionales son verdades para solamente algunos valores de las variables implicadas:
); tales ecuaciones son llamadas identidades. Las ecuaciones condicionales son verdades para solamente algunos valores de las variables implicadas:  . Los valores de las variables que hacen la ecuación verdadera se llaman las soluciones de la ecuación.
. Los valores de las variables que hacen la ecuación verdadera se llaman las soluciones de la ecuación.martes, 28 de septiembre de 2010
martes, 21 de septiembre de 2010
Suscribirse a:
Comentarios (Atom)